Instantaneous Frequency Estimation

Instantaneous Frequency (IF) estimation of a frequency modulated (FM) signal plays a key role in several areas such as radar, speech and music analysis, surveillance etc.. The problem consists of estimating the (positive) value of the local frequency:

Φ'(t) = ∂Φ(t) / ∂t

of the time-depedent (FM) signal

f(t)= a(t)cos(Φ(t))

with amplitude a(t). Such a problem is not trivial for multicomponent signals:

f(t) = ∑k=1K ak(t) cos(Φk(t))      K ∈ N ,

as there are various and close spectral components.

 

  An example of multicomponent signal is shown below:

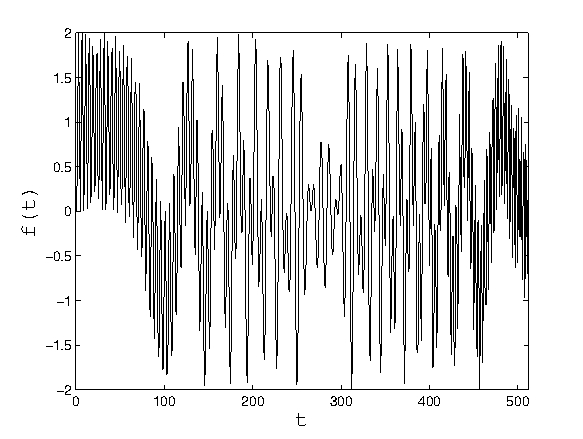FM multicomponent signal 

 

In practice, there are many applications where the interference of FM signals plays a key role to design specific frameworks, such as cellular systems, satellite systems, optical fibers etc..

This is the reason why several time-frequency transform based approaches have been proposed in the literature:

 

 

  There are many papers on this topic. See for instance:

  1. I. Djurovic, P. Wang, C. Ioana, Modification of the robust chirp-rate estimator for impulse noise environments, Signal Processing, 90(5), pp. 1730-1736, May 2010.
  2. A. Akan, L. F. Chaparro, Evolutionary chirp representation of non-stationary signals via Gabor transform, Signal Processing, 81(11), pp. 2429-2436, Nov. 2001.
  3. I. Djurovic, L. Stancovic, J. F. Bohme, Estimation of FM signal parameters in impulse noise environments, Signal Processing, 85(4), pp. 821-835, April 2005.
  4. Y. Wei, G. Bi, Broadband interference suppression in DS-SS system with modified discrete chirp Fourier transform, Signal Processing, 84(10), pp. 1749-1758, Oct. 2004.
  5. M. Sahmoudi, K. Abed-Meraim, Multicomponent chirp interference estimation for communication systems in impulsive α-stable noise environment, Proc. of First International Symposium on Control, Communications and Signal Processing, pp. 299-302, Sept. 2004.
  6. W.-H. Ng, Investigation of chirp interference on RAC demodulation, Electronics Letters, 25 (17), pp. 1165 - 1167, Aug. 1989.
  7. M. Stefanovic, P. Spalevic, D. Martinovic, M. Petrovic, Comparison of Chirped Interference Influence on Propagation Gaussian and Super Gaussian Pulse along the Optical Fiber, Journal of Optical Communications, 27(6), pp. 305-309, 2011.
  8. E. Sejdic, I. Djurovic, L. Stankovic, Quantitative Performance Analysis of Scalogram as Instantaneous Frequency Estimator, IEEE Trans. on Signal Processing, 56(8), pp. 3837-3845, Aug. 2008.
  9. H. K. Kwok, D. L. Jones, Improved Instantaneous Frequency Estimation using a Adaptive Short-Time Fourier Trasnform, IEEE Trans. on Signal Processing, 48(10), pp. 2964-2972, Oct. 2000.
  10. I. Sarkar, A. T. Fam, The interlaced chirp Z transform, Signal Processing, 86(9), pp. 2221-2232, Sept. 2006.
  11. X. Li, G. Bi, The Reassigned Local Polynomial Periodogram and its Properties, Signal Processing, 89 (2009) 206-217.
  12. X. Li, G. Bi, S. Stankovic, A. M. Zoubir, Local Polynomial Fourier Transform: A Review on Recent Developments and Applications, Signal Processing, 91 (2011) 1370-1393.
  13. L. Angrisani, M. D'Arco, A Measurement Method based on a Modified Version of the Chirplet Transform for IF Estimation, IEEE Trans. on Instrum. and Meas., 51(4), pp. 704-711, Aug. 2002.
  14. E. Sejdic, L. Stankovic, M. Dakovic, J. Jiang, Instantaneous Frequency Estimation Using the S-Transform, IEEE Signal Processing Letters, 15, pp. 309-312, Feb. 2008.
  15. I. Djurovic, L. Stankovic, Robust Wigner Distribution with Application to the Instantaneous Frequency Estimation, IEEE Trans. on Signal Processing, 49(12), pp. 2985-2993, Dec. 2001.
  16. B. Barkat, L. Stankovic, Analysis of polynomial FM signals corrupted by heavy-tailed noise, Signal Processing, 84(1), pp. 69-75, Jan. 2004.
  17. P. Wang, H. Li, B. Himed, Performance of Instantaneous Frequency Rate Estimation using High-Order Phase Function, IEEE Trans. on Signal Processing, 58(4), pp. 2415-2421, Aug. 2010.
  18. L. Weruaga, M. Kepesi, The fan-chirp transform for non stationary harmonic signals, Signal Processing, 87(6), pp. 1504-1522, June 2007.
  19. F. Auger, P. Flandrin, Improving the Readability of Time-Frequency and Time-Scale Representations by the Reassignment Method, IEEE Transactions on Signal Processing, 43(5), pp. 1068-1089, May 1995.

  For an extensive review, see:

  1. S. Mallat, A Wavelet Tour of Signal Processing, Academic Press, 1998.

  2. B. Boashash, Estimating and Interpreting the Instantaneous Frequency of a Signal - Part 1: Fundamentals and Part 2: Algorithms and Applications, Proc. IEEE, 80(4), pp. 520-568, April 1992.