Formal Equivalence between

Jensen-Shannon Divergence and Michelson Contrast

Introduction

OBJECTIVE

To investigate about the existence of a formal relation between the entropy cost of an object of a real-world scene (an image I) and its visual cost.

STRATEGY

We restrict to the class of linear distortions (α I(x,y) + β) and to the Michelson contrast [1] as effective and mathematically tractable tools. The formal link between the relative entropy, i.e., the Jensen-Shannon Divergence (JSD) [2][3], and the Michelson contrast relies on the ''relative'' nature of visual contrast --- an object is detected if it is different from its surrounding information.

RESULTS

It is proved that JSD increases as image distortion increases, while it is not so for image entropy;

JSD combined with Michelson contrast is able to provide a universal visibility threshold (TJS1) that is independent of distortion parameters. It only depends on the Just Noticeable Threshold ε of Michelson contrast.

In particular:

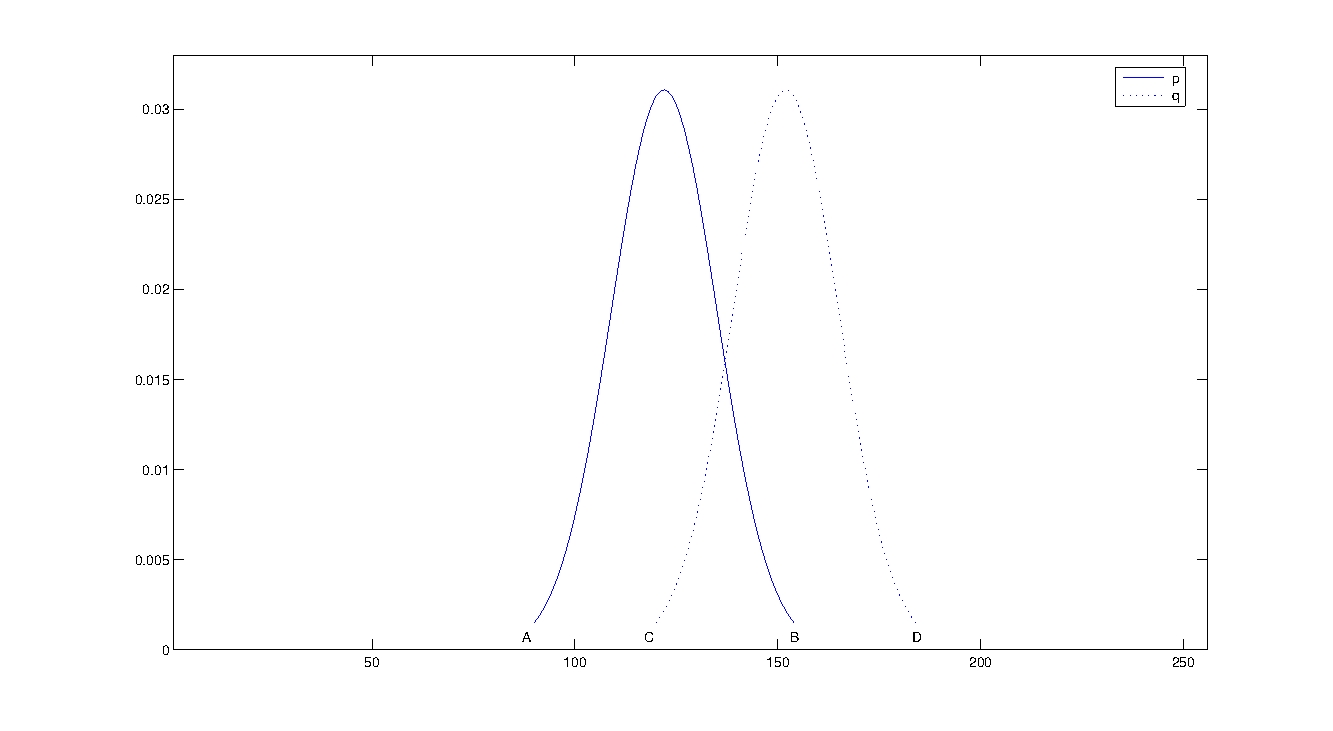
A linear distortion of a certain region of the I changes image p.d.f. from p to q , as shown in the following Figure:

The behavior of the Michelson contrast (x) and the Jensen-Shannon divergence (solid) for different values of α and β, where '+' indicates the lower ( 1 - ε ) and upper ( 1 + ε ) bounds for the visual contrast of regions containing an unvisible stimulus, is depicted in the following figure

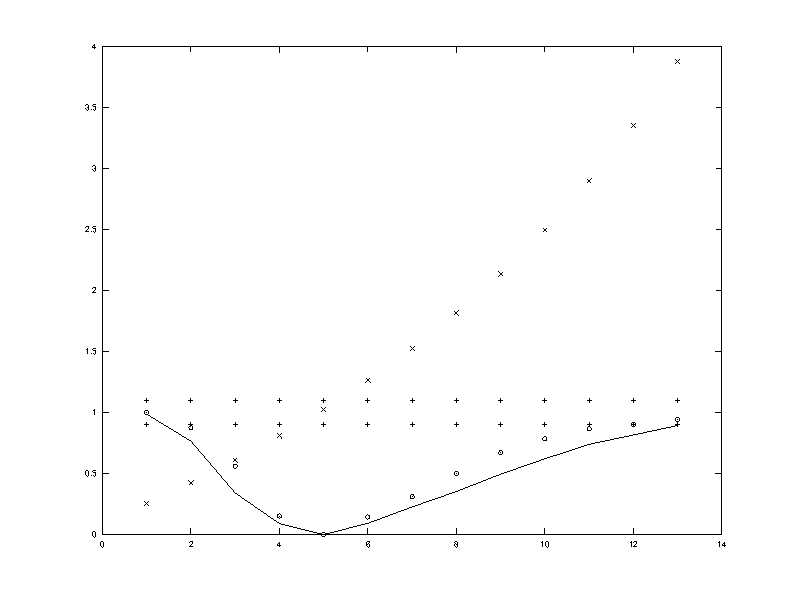
The absolute minimum of the JSD corresponds to a Michelson contrast (MC) equal to 1. However, a little tolerance ε can be left to the MC as the Human Visual System is not able to detect this stimulus.

Which is the corresponding cost in terms of bpp?

It can be proved that this cost corresponds to two thresholds TJS1 ( ≥ 1 ) and TJS2 ( α < 1 ), due to the asymmetry of JSD (see again the Figure above). But it can be also proved that

TJS1 ≤ TJS2

Hence, the least universal threshold TJS1 represents the bits budget granted to a given distortion to be not a stimulus for HVS without any additional information about the distortion (i.e. α <, = or > 1).

ADVANTAGES

The proposed model does not make any assumption about image statistics;

The proposed model does not have the computational burden of multiscale transforms.

Some results can be found below while more details and proofs can be found in [4].

Some Experimental Results

1st set of examples:

CAMPBEL-ROBSON CHART


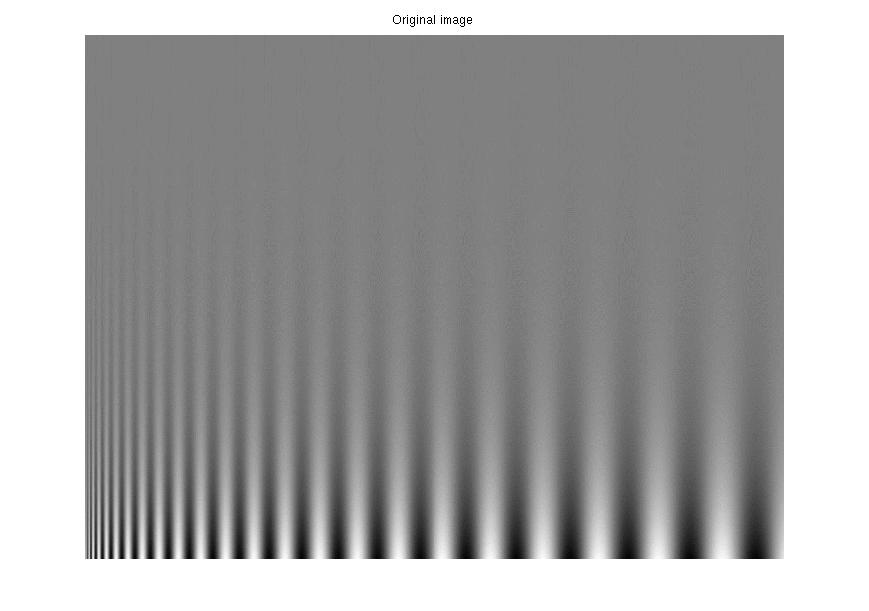
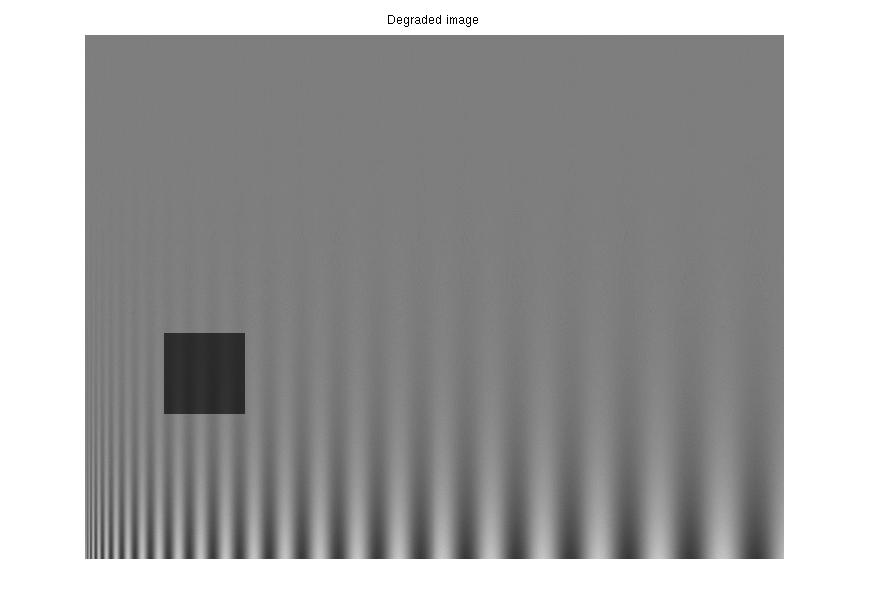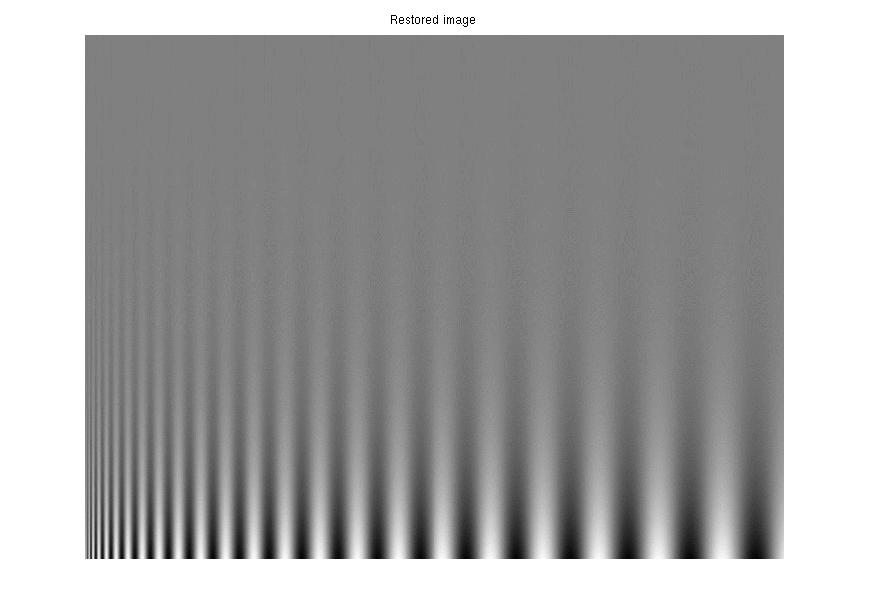1st synthetic distortion: α =.5, β=-17.5, m = 35.	Restored*: α=.997, β=-.1050, m = 35. TJS1 = .0004, TJS2 = .0004.
*Due to limitations of web browsers, all images are exported from matlab with JPEG at the highest quality for display in the browser. However, since the highest quality level is used, this should have a little effect on their perceived quality. Anyway, all experiments can be reproduced by the matlab codes at bottom of this page.

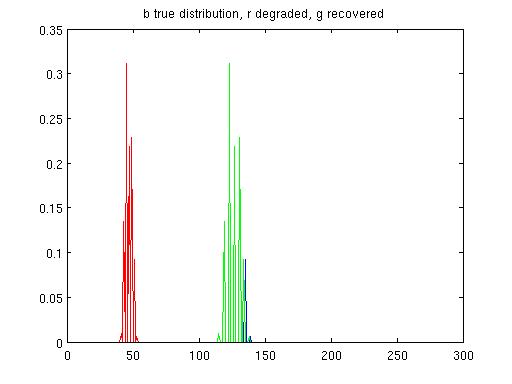
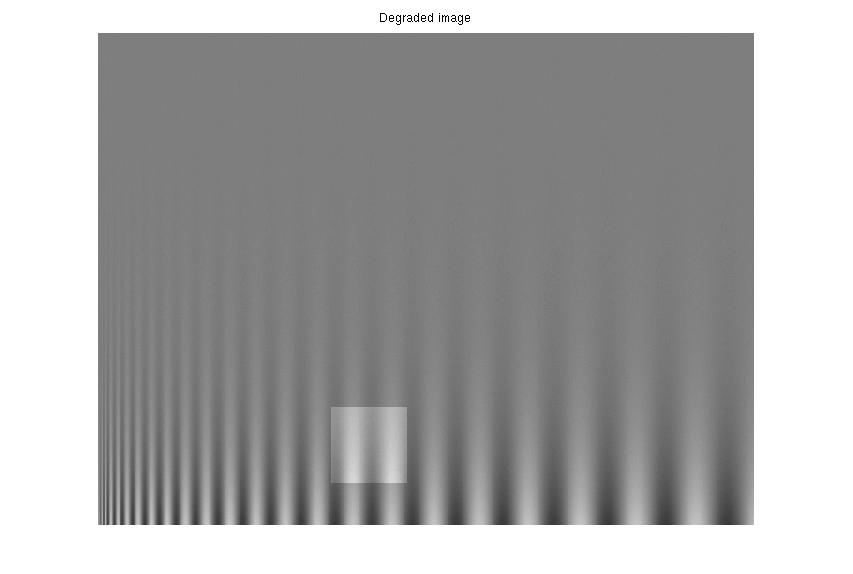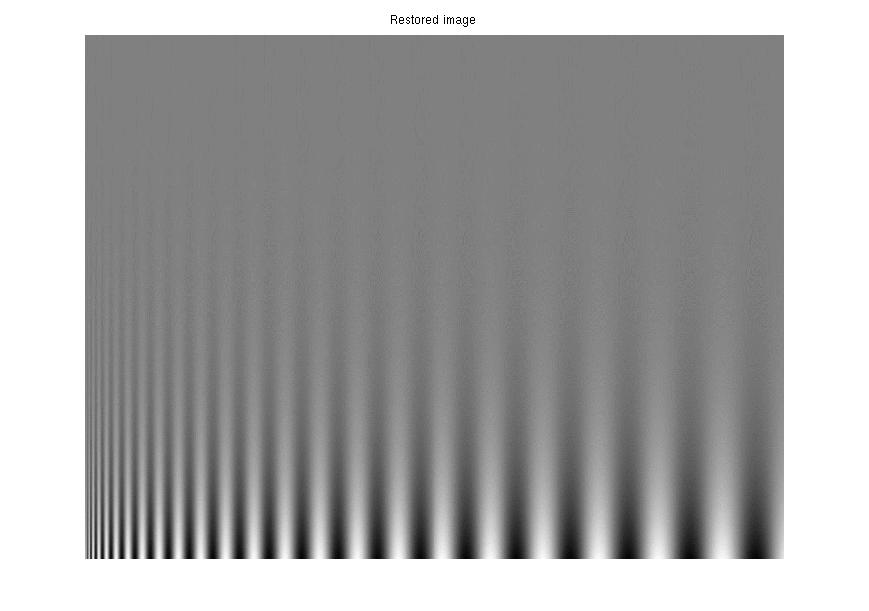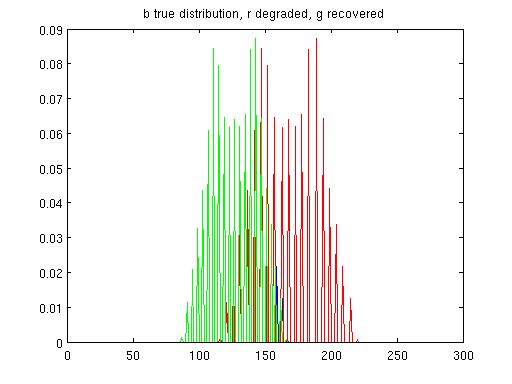
Their empirical p.d.f.s: The 'true' distribution is extracted from the same block in the original image.


2nd synthetic distortion: α=1.3, β=3, m = 10.	Restored: α=.997, β=-.03, m = 10. TJS1 = .0001, TJS2 = .0001.

Their empirical p.d.f.s.


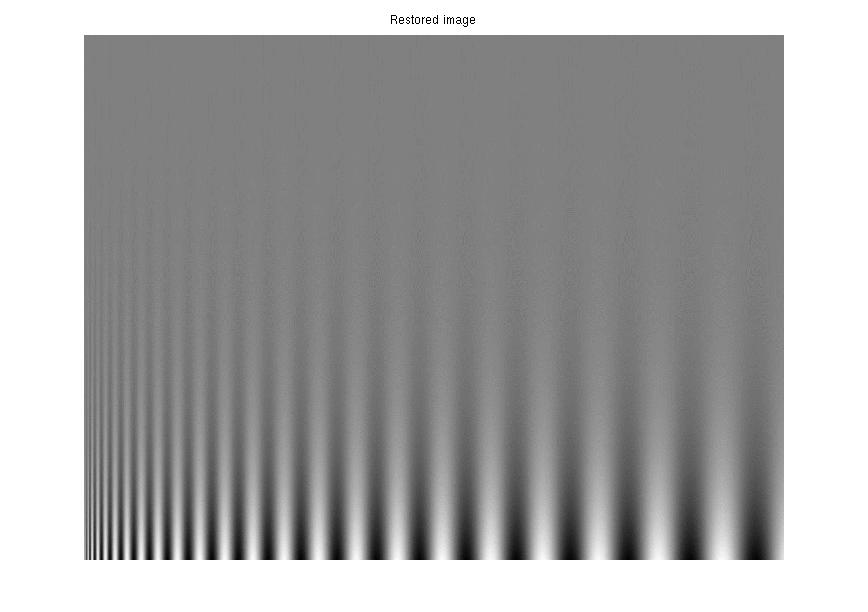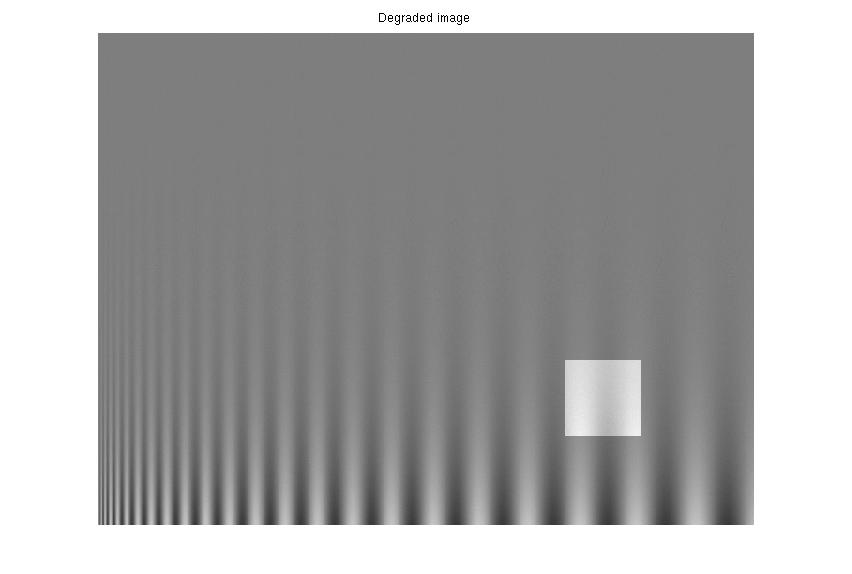
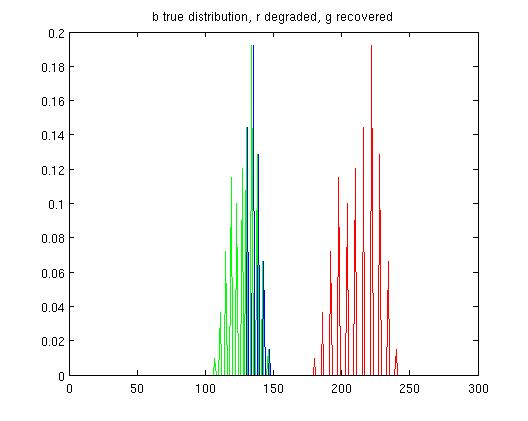
3rd synthetic distortion: α==1.5, β=20, m = 40.	Restored: α=.997, β=-.12, m = 40. TJS1 = .0005, TJS2 = .0005.

Their empirical p.d.f.s.

2nd set of examples*:

*All images of this set are from [5].

Straw (Brodatz)

Original Image


Synthetic distortion: α =.7, β=-1.5, m = 5.	Restored: α=.96, β=-.2, m = 5. TJS1 = .0008, TJS2 = .0008.

Empirical p.d.f.s.

Bark (Brodatz)

Original Image


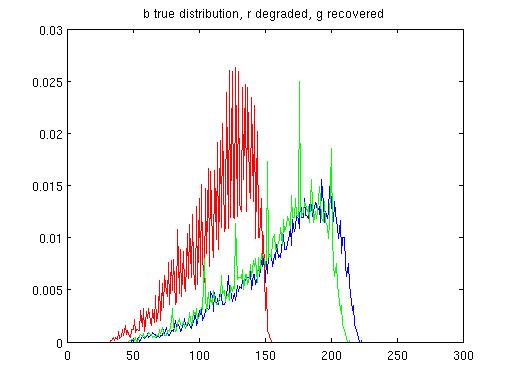
Synthetic distortion: α =.6, β=-6, m = 15.	Restored: α=.97, β=-.45, m = 15. TJS1 = .0020, TJS2 = .0020.

Empirical p.d.f.s.

Wood fence

Original Image


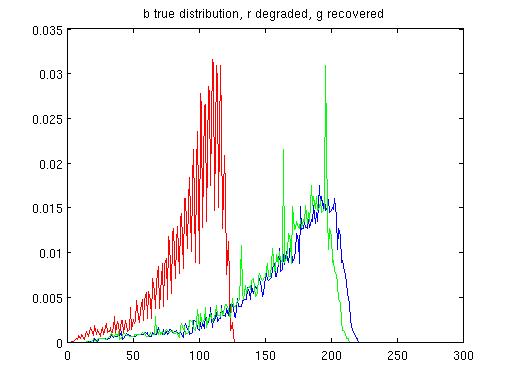
Synthetic distortion: α =1.3, β=4.5, m = 15.	Restored: α=.98, β=-.3, m = 15. TJS1 = .0013, TJS2 = .0013.

Empirical p.d.f.s.

Rough wall

Original Image


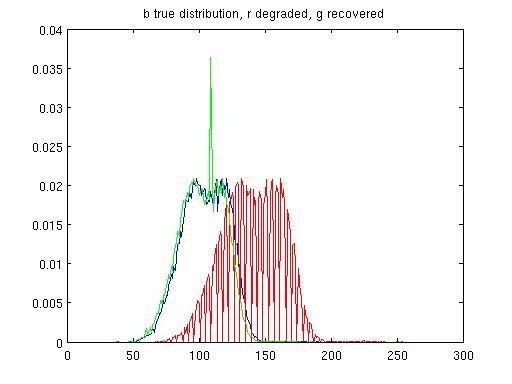
Synthetic distortion: α =.6, β=-2, m = 5.	Restored: α=.96, β=-.2, m = 5. TJS1 = .0007, TJS2 = .0007.

Empirical p.d.f.s.

3rd set of examples:

REAL IMAGES WITH A SYNTHETIC DEGRADATION: ARCHIVE MANUSCRIPT


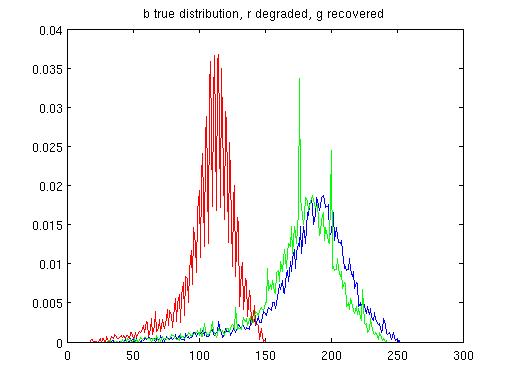
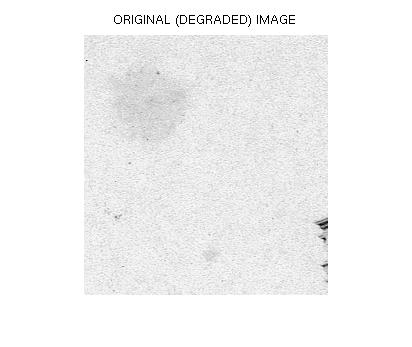
Original Image: Manuscript initially degraded by a semi-transparent Blotch.	Synthetic distortion: α =.7, β=-3, m = 10.

1st Restoration (unvisible): α =.97, β=-.3, m = 10. TJS1 = .0014, TJS2 = .0014.	2nd Restoration (slightly visible): α=.94, β=-.6, m = 10. TJS1 = .0028, TJS2 = .0029*. Note that TJS1 is not equal to TJS2 in this case, while their behavior tends to coincide for a decreasing visibility of the distortion --- i.e. in most practical cases where an unvisible restoration is achieved.

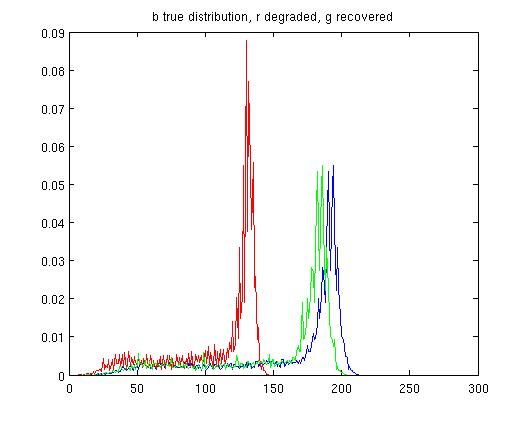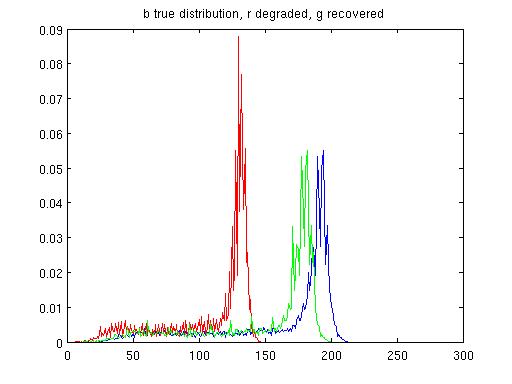Empirical p.d.f.s. of 1st restoration	Empirical p.d.f.s. of 2nd restoration

4th set of examples:

REAL IMAGES WITH A REAL DEGRADATION: DEGRADED ARCHIVE PHOTOS*

*All images of this set are from Alinari Archive.

Original Image: Isolated Blotch. DJS = .2786


Region where to compute the distortion p.d.f. q.	Region where to compute the (supposed) original p.d.f. p. It has been achieved by dilating [6] the mask on the left and then subtracting it.

1st Restoration [7]: DJS = .1064, TJS1 = .0048.	2nd Restoration [8]: DJS = .1631, TJS1 = .0243.

3rd Restoration [9]: DJS = .1545, TJS1 = .0250.

Original Image: Blotch on Church. DJS = .1027


Region where to compute the distortion p.d.f. q.	Region where to compute the (supposed) original p.d.f. p.

1st Restoration [7]: DJS = .0364, TJS1 = .0297.	2nd Restoration [8]: DJS = .1070, TJS1 = .0538.

3rd Restoration [9]: DJS = .0903, TJS1 = .0590.

Original Image: New Isolated Blotch. DJS = .3316.

Restoration: DJS=.2523, TJS1 =.0365.

REFERENCES:

S. Winkler, Digital Video Quality, Vision Models and Metrics, Wiley, 2005.
J. Lin, Divergence Measures based on the Shannon Entropy, IEEE Trans. on Information Theory, Vol. 37, No. 1, Jan. 1991.
D. M. Endres, J. E. Schinelin, A New Metric for Probability Distributions, IEEE Trans. on Information Theory, Vol. 49, No. 7, July 2003.
V. Bruni, E. Rossi, D. Vitulano, On the Equivalence between Jensen-Shannon Divergence and Michelson Visual Contrast, submitted to IEEE Trans. on Information Theory.
USC-SIPI image database
R. C. Gonzalez, R. E. Woods, Digital Image Processing, Prentice Hall, 2nd Edition, 2002.
V. Bruni, A. J. Crawford, A. Kokaram, D. Vitulano, Semi-transparent blotches removal from sepia images exploiting visibility laws, Signal, Image and Video Processing, Springer-Verlag, Online First DOI 10.1007/S11760-011-0220-1, 2011.
F. Stanco, L. Tenze, G. Ramponi, Virtual Restoration of Vintage Photographic Prints Affected by Foxing and Water Blotches. Journal of Electronic Imaging, Vol. 14, No. 4, Dec. 2005.
A. Greenblatt, S. Agaian, K. Panetta, Restoration of Images Damaged by Semi-Transparent Water Blotches using Localized Image Enhancement, Mobile Multimedia/Image Processing, Security, and Applications 2008. Edited by Agaian, Sos S.; Jassim, Sabah A. Proceedings of the SPIE, Volume 6982, pp. 69820V-69820V-10, 2008.

MATLAB CODE:

Matlab code to produce a squared synthetic distortion on any (gray-level) image you like and to measure the corresponding Michelson contrast, Jensen-Shannon divergence as well as TJS1 and TJS2: sintjs.m code , Campbel-Robson chart and Manuscript .
Matlab code to to measure the corresponding Michelson contrast, Jensen-Shannon divergence as well as TJS1 and TJS2 between the degraded and restored image on a local distortion: realjs.m code and restorations of isolated blotch: isoall.mat , blotch on Church: cupleall.mat , new isolated: newiso.mat